Instructional Routines
“Specific and repeatable designs for learning that support both the teacher and students in the classroom.”
Which One Doesn’t Belong?
Students classify objects by their attributes and properties to create sets that belong together.
Invites students to compare, explain and justify.
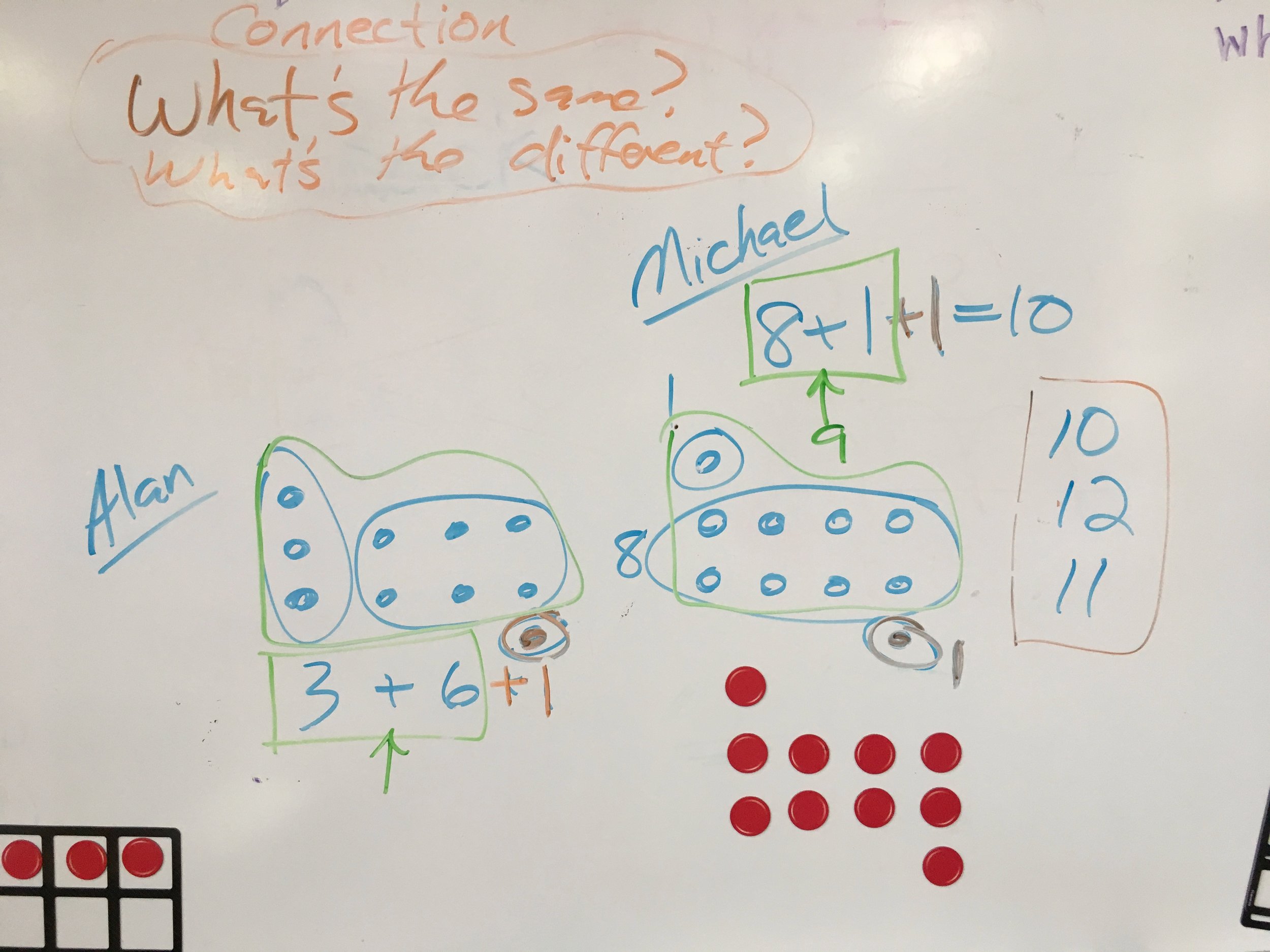
Dot Talks
Students compose, decompose, rearrange quantities of dots to build number sense.
Invites students to explain, represent, and critique.
Contemplate Then Calculate
Similar to Dot Talks, this Routine for Reasoning “fosters structural thinking, math practice 7.”
Invites students to describe, represent, and interpret.
Choral Counting
Students build reasoning of base-ten number system, fractions, measurement by counting, noticing patterns, and predicting.
Invites students to describe, justify and generalize.
Counting Collections
Students organize objects and come up with efficient strategies for counting. Students develop their reasoning for counting and build a foundation of the base-ten number system.
Invites students to explain, describe and represent.
Number Talks
Students build fluency and flexibility with numbers and operations by mentally computing. Students compose, decompose and rearrange numbers symbolically and visually.
Invites students to explain, represent, and compare.
Mathematical Language Routine “Three Reads”
To help students read math problems like mathematicians. This routine supports reading comprehension, sense-making, and meta-awareness of mathematical language.
Mathematical Language Routine “Compare & Connect”
Students develop meta-awareness of multiple mathematical approaches and representations, as well as have mathematical conversations.
Prompts such as “What is the same? What is different?” supports students to compare. “Where do you see ___ in ___?” supports students to make mathematical connections.
Mathematical Language Routine “Co-Craft Questions”
Students use conversation skills to generate mathematical questions about a situation before asking students to produce answers to pre-determined questions. This routines lets students understand the context of the problem and attend to the details before doing problem solving begins. Students themselves produce the language of mathematical questions, like all mathematicians do.
Mathematical Language Routine “Collect & Display”
This routine captures students’ oral words and phrases into a written collective reference (including both words and pictures) for all to use. Students’ mathematical language becomes more precise.
Mathematical Language Routine “Stronger & Clearer Each Time”
Students get a chance to have first draft thinking for a math problem. Through successive partner shares, all students revise and refine both their mathematical thinking and their language. During these opportunities for feedback, students borrow ideas and language to build a stronger and clearer next draft.